#basics of logarithms
Explore tagged Tumblr posts
Text
logarithms are an affront to God
#you put this word in front of a number and it magically returns the exponent needed to get to that number?#sounds fake#this is mostly joking btw like i do know what logarithms do but in a very abstract way and every time they come up in a class#i basically have to relearn them#they make less sense to me than derivatives and integrals btw#file this under i may be stupid
6 notes
·
View notes
Text
youtube
In this video, we delve into the art of solving logarithmic equations with different bases, demystifying the process for you step by step. Whether you're a student brushing up on logarithms or someone facing more complex problems, we've got you covered. Understanding how to work with different bases is crucial when faced with logarithmic equations. We break down the techniques, providing clear explanations using frequently used words to ensure that you grasp the concepts effortlessly. No more getting stuck on those seemingly perplexing logarithmic problems!
#Different bases for solving a log equation#logarithm questions basic#tricky logarithmic questions solve#logarithm formula#solving logarithms#logarithm base#logarithm applications#evaluate basic logarithm#formula of logarithms#solving logarithmic equations#logarithms explained#how to simplify logarithms#solving negative exponents#free math videos#logarithmic#algebra#mathematics#tutorial#Sami’s A Plus#sami’s a plus#math lessons#math for kids#learn math fast#Youtube
2 notes
·
View notes
Note
hiii can you do kimi antonelli asking help from a cute girl in his class or a driver’s younger sister to tutor him in math?
LISTEN UP NOW!
FORMULA ONE DRIVER X READER

Summary: Kimi asks his cute classmate for help with math!
Warnings: Silly, fluff, Y/N usage, user is in last year of high school
Featuring: Kimi Antonelli x Classmate!Reader
REQUESTS OPEN! Check here for more info!
Still getting to requests today, but feel free to send some in! Love y’all
Nobody necessarily expected Kimi Antonelli to still be in school. Rarely did you see a Formula One driver who was still learning about the basics, such as math and language, while also simultaneously passing world champions in their sport and making a living for themselves. After this information came out, there was obviously… Quite a few jokes.
Kimi had made a whole ordeal of asking George to tutor him in math, and while viewers (and George himself) passed it off as a joke, the truth was Kimi really was struggling in the subject. It didn’t have much substance to him, and lacked sense. Unlike racing, which came so naturally to the rookie.
His teachers were emailing him nonstop, scolding the racer on how unbalanced his school life and work life were. Despite being a kid who raced cars for a living, going at unimaginable speeds, he still walked away with his tail tucked between his legs after being harshly lectured by his elders. After being reprimanded for about the thirtieth time, Kimi was instructed to find himself a tutor.

Online class was easy. Everyone was given their own workload to finish at their own pace, with varying deadlines depending on level of learning. Y/N excelled in this department, finishing most of her work far before the others. She was a straight A student, sitting at the top of her class.
On rare occasions, their class would host little lessons over Zoom. It always reminded her of the quarantine days, but it was nice to see familiar faces nonetheless. Even if most of the time she was sat there quietly, watching everyone else get caught up with the work.
One evening, a surprise guest had popped up. Andrea Kimi Antonelli, whom had never had enough time to make an appearance. Everyone knew of him— Y/N would be stupid if she didn’t. Of course, the reaction to his involvement was rather distracting to the sake of the course, but it was entertaining nonetheless.
He seemed lost the entire time, barely able to answer basic questions about logarithm and pythagorean theorem— Things they had actually learned during the prior years. Being an F1 driver must really be time consuming. Once the call was over, she did what a typical, compassionate person would do…
Offered her assistance!

Y/N’S MESSAGES ☆




Every night, right after Kimi had finished up his responsibilities as an F1 driver, he’d stop by the hotel room his team had booked for Y/N, his new tutor. Every time, without fail, he’d find her sitting at the hotel desk, finishing up any new work the moment it came out. It was endearing how dedicated to school she was.
At first, their meetings were strictly professional. She’d teach him the basics, and then he’d be on his way. But by the fourth night of tutoring, the air had become more friendly. He brought in leftover food from the after party, which they shared while watching the newest episode of whatever reality TV show was airing on the hotel TV.
Y/N found herself craving his company by now. She counted down the minutes until she would see Kimi again, eager to spend as much time as possible with the aspiring racer. He was charming, funny, and… Despite his mishaps, intelligent nonetheless.
The week of her traveling came to an end, and the two parted ways at the airport before her flight back home to Italy.

your.username
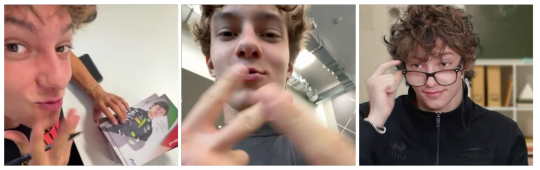
liked by kimi.antonelli and others
your.username Tutored this dork, learned about F1, and watched my first race in person… Eventful week.
tagged kimi.antonelli
—
classmate.user1 - Not fair that Y/N and Kimi are out having fun while we’re stuck here!
♥︎ by author
classmate.user2 - Agreed 😐
> kimi.antonelli - Should have offered to tutor a friend in need!!
♥︎ by author
friend.user1 - Jealous!! But we missed you here in Italy 🇮🇹
♥︎ by author
friend.user2 - Did you get to meet any of the other drivers?
♥︎ by author
your.username - Lewis Hamilton himself…
> friend.user2 - I HATE YOU I’M JEALOUS
♥︎ by author
friend.user3 - Woah…
your.username - ??
kimi.antonelli - Miss you already! My grade already went up!
♥︎ by author

Y/N’S MESSAGES ☆


#f1 x reader#f1 smau#formula 1#formula one#f1#f1 fanfic#f1 fic#f1 fluff#f1 imagine#ka12#ka12 x reader#kimi antonelli x reader#kimi antonelli#kimi antonelli fic#kimi antonelli fluff
607 notes
·
View notes
Text
i've been busy the whole day, so i just now got around to watching s4 ep2 of black butler, and i—

hit me with it.

why do you look like a kicked puppy? my pussy's right here to make u feel better!!!

fuck me.

just go ahead and take the thing off for me hm?

PLEASEPLEASEPLEASE LOOK AT ME LIKE THAT

IDC HOW BASIC THIS TROPE IS, RAIL ME IN THE CONFESSIONAL RN. RIGHT. NOW. MY PUSSY IS WET AND READY FOR DEMON DICK.






no lube, no protection, all night, all day, from the kitchen floor to the toilet seat, from the dining table to the bedroom, from the bathroom sink to the shower, from the front porch to the balcony,vertically, horizontally, quadratic, exponent al, logarithmic, while i gasp for air, scream and see the light, missionary, cowgirl, reverse cow girl, doggy, backwards, forwards, sideways, upside down, on the floor, in the bed, on the couch, on a chair, being carried against the wall, outside, in a train, on a plane, in the car, on a motorcycle, the bed of a truck, on a trampoline, in a bounce house, in the ool, bent over, in the basement, against the window, have the most toe curling, back arching, leg shaking, dick thribbing, first clenching, ear rining, mouth drooling, ass clenching, nose sniffling, eye watering, eye rolling, hip thrusting, earthquaking, sheet gripping, knuckles cracking, jaw dropping, hair pulling.teeth jitterbug, mind blogging, soul snatching, overstimulating, vile, sloppy, moan inducing, heart wrenching, spine tingling, back breaking, atrocious, gushy, creamy, beastly, ip bitting, gravity defying, nail biting, sweaty, feet kicking, mind blowing, body shivering, orgasmic, bone breaking, world ending, black hole creating, universe destroying, devious, scrumptious, amazing, delightful, delectable, unbelievable, body numbing, bark worthy, cant walk, head nodding, soul evaporating, volcano erupting, sweat rolling, voice cracking, trembling, sheets soaked, hair drenched, flabbergasting, lip locking, skin peeling, eyelash removing, eye widening, pussy popping, nail stractching, back cuts, spectacular, brain cell desolving, hair ripping, show stopping, magnificent, unique, extraordinary, slendid, phenomenal, mouth foaming, heavenly, awakening, devils tangos, he could put a nuclear bomb inside me and i'd still ride.

I NEED HIM!!
+ bonus, a pretty boy

#( the yapper in me )#this is thirst the#sebastian michaelis#sebastian michaelis smut#sebastian michaelis x reader#sebaciel dni#anti sebaciel#kuroshitsuji#black butler#black butler public school arc#i said i was gonna lose it when this episode came out#and this is tame.
1K notes
·
View notes
Note
Can you do one about the Sea of Thieves water?

OK
so . there was a biiig long talk about this at siggraph one year!! you can watch that here if you'd like . in the time between me getting this ask and me fully recreating the water, acerola also released a great video about it . the biiig underlying thing they do and the reason why it looks so good is they are making a Really Detailed Ocean Mesh in realtime using something called an FFT (fast fourier transform) to simulate hundreds of thousands of waves, based on a paper by TESSENDORF
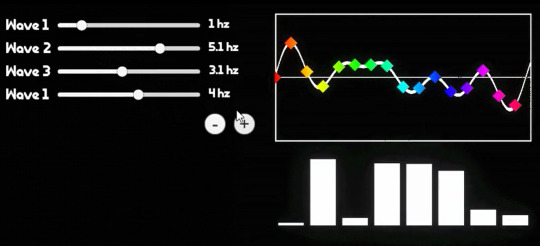
WHAT IS AN FFT - we'll get to that. first we have to talk about the DFT - the discreet fourier transform. let's say you have a SOUND. it is a c chord - a C, an E, and a G, being played at the same time. all sounds are waves!!! so when you play multiple sounds at the same time, those waves combine!!! like here: the top is all 3 notes playing together, so they form the waveform at the bottom!!
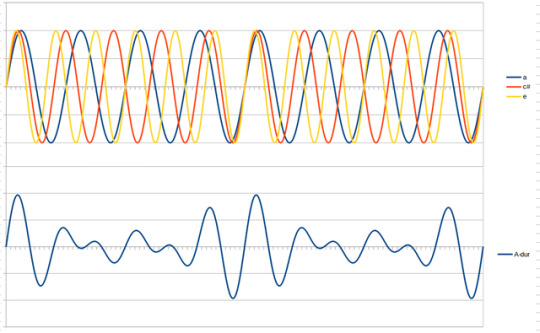
now if someone handed you the bottom wave, could you figure out each individual note that was being played? how about if someone handed you a wave of One Hundred Notes. you would think it would be very hard. and well, it would be, if not for the Discreet Fourier Transform.
essentially, there is a way to take a bunch of points on a waveform comprised of a bunch of different waves, add them all together, do some messed up stuff with imaginary numbers, that will spit back out at you what individual waves are present. i made a little test program at the start of all this: the left are the waves i am putting into my Big Waveform, the top right is what that ends up looking like, and all the little rainbow points on it are being sampled to spit out the graph at the bottom right: it shows which frequency bands the DFT is finding (here it is animated)
this has enormous use cases in anything that deals with audio and image processing, and also,
THE OCEAN
tessendorf is basically like, hey, People Who Are Good At The Ocean say that a buuuunch of sine waves do a pretty good job of approximating what it looks like. and by a bunch they mean like, hundreds of thousands to millions. oh no.... if only there was a way we could easily deal with millions of sine waves..........
well GREAT news. not only can you do the DFT in one direction, but you can also do it in REVERSE. if you were to be given the frequency graph of a noise for example, you could use an INVERSE DFT to calculate what the combined wave graph looks like at any given time. so if you were to have say, the frequency graph of an oceaaaan, for example, you could calculate what the Ocean wave looks like at any given time. and lucky for us, it works in two dimensions. and thats the foundation of the simulation !!!!!
BUT WAIT
as incredible as the DFT is, it doesn't scale very well. the more times you have to do it, the slower it gets, exponentially, and we are working with potentially millions of sine waves here
THE FAST FOURIER TRANSFORM here we are . the fast fourier transform is a way of doing the discreet fourier transform, except, well, fast. i am Not going to explain the intricacies of it because its very complex, but if you want to learn more there are a ton of good 30 minute long videos on youtube about it . but essentially, due to the nature of sine waves repeating, you can borrow values as you go, and make the calculation Much faster (from exponential growth to logarithmic growth which is much much slower, and scales very well at higher numbers). it's, complicated, but the important part is it's so much faster and the diagram kind of looks like the shadow the hedgehog story plot
so if we use the inverse FFT on a graph of a rough estimate of what frequency of waves in the ocean (called a spectrum, basically tells us things like how many small waves, how many big waves, how different waves follow the wind direction. sea of thieves uses one called the phillips spectrum but there are better ones out there!!) now we have our waves !!!!!!! we can also use another inverse FFT to get the normals of the waves, and horizontal displacement of the waves (sharpening peaks and broadening valleys) through some derivatives . yayy calculus
OK MATH IS OVER. WE HAVE OUR WAVES!!! they are solid pink and look like pepto bismol. WHAT NOW

i cheated a bit here they look better than not being shaded because i am using the normals to reflect a CUBEMAP to make it look shiny. i think sea of thieves does this too but they didnt mention it in their talk. they did mention a FEW THINGS THEY DID THOUGH
FIRST OFF - SUBSURFACE SCATTERING. this is where the sun pokes through since water is translucent. SSS IS REALLY EXPENSIVE !!!!!! so they just faked it. do you remember the wave sharpening displacement i mentioned earlier? they just take the value where the waves are being sharpened and this will pretty naturally show off the areas that should have subsurface scattering (the sides of waves). they make it shine through any time you are looking towards the sun. they also add a bit of specular ! sss here is that nice blue color, and specular is the shiny bits coming off the sun. the rest of the lighting is the cubemap i mentioned earlier, i dont know if thats what they use but it looks nice !!!!!

then the other big thing that they do is the FOAM !! sorry i lied. there's more math. last one. you remember the wave sharpening displacement i Just mentioned. well they used that to find something called the JACOBIAN and well im not even going to begin to try and explain what it means but functionally what it does, is when the jacobian is NEGATIVE it means waves are clipping into eachother. and that means we should draw some foam!!! we can also blur and fade out the foam texture over time and continuously write to it to give it some movement, and bias this value a bit to make more or less foam. they do both of these!!!

YAYYYYY !! OK !! THAT'S SEA OF THIEVES WATER!!!!! THANKS FOR WAITING ALL THIS TIME. you can see my journey here if you would like to i have tagged it all oceanquest2023
thank you everyone for joining me :) i had fun
1K notes
·
View notes
Text

friday 10/05/24
basic logarithms! had a solid revision day, but it was super rainy!!
♫ misses - dominic fike ♫
#studyblr#studyspo#study aesthetic#stem#studying#women in stem#aesthetic studying#study motivation#aesthetic#studystudystudy#soft academia aesthetic#dark academia aesthetic#soft academia#academia#chaotic academia#poc dark academia#stem academia#light academia#dark academia#academia aesthetic#math aesthetic#mathblr#math#study inspiration#study vibes#study study study#study hard#study#logarithms#logaesthetic
219 notes
·
View notes
Text
A True Friend
Caspian Keyes X GN!Reader
Word Count: 776
Requested: Anon @kalebell46
Request: On god please I need more Caspian Keyes fan fiction. This internet is so dry, there's like none out there. Could be of a him x reader while he's finding himself, the first real friend in his life that isn't there by the choice of someone else. And he'd be so paranoid about it too. Gooooodddddd please. AND I would love for a caspian fic please there are none

Caspian had been alone for so long, since he was young he had always been the outsider, the black sheep, the target and he thought that was how it was going to be for the rest of his school life. That is until he met (Y/N). Now (Y/N) for all intents and purposes probably wasn’t the best example for Caspian, they got into trouble, paid around and never listened to anyone who assumed that they knew better than them. Except when they were with Caspian, who they had only met because they needed tutoring.
(Y/N) wasn’t stupid though most people treated them that way, in fact they had a basic grasp on most things that were taught in class, they just didn’t seem to get it down on paper very well. Caspian was asked to tutor them and the rest followed with time, tutoring sessions turned into skateboard races and trips to the comic book store. Caspian learned quickly that his new companion was not stupid as he had heard a lot of the others in their year saying so he did make sure that some of their time was dedicated to bringing up his grades, in the end it didn’t matter though.
The world crumbled around Caspian as he found out about the real reason behind his birth, with his father gone and his mother keeping more of a watchful eye on him then usual, the only place he thought he might even be a little bit safe was with (Y/N) but then the thought crossed his mind… What if you had something to do with Logarithm's little experiment. That was why he stood outside your door hand hovering to knock, he jumped when you opened it smiling at him “what are you doing?” They asked “thought you were going to knock but you seemed like you were thinking about something.” They stepped to the side giving him space to come in but he didn’t move. “What?” “Are you really my friend?” He asked. “Really your friend?” They asked “of course I am.” “Really because I just found out a lot about myself that doesn’t make sense.” He answered. “Okay talk me through it.” They prompted stepping out and closing the door behind them. “I found something on my computer, they’ve been watching me.” Caspian answered. “They’ve been watching you?” They asked frowning, you were either genuinely confused or very good at acting. “Logarithms!” He answered more frustrated at having to explain himself at all. “Logarithms? Caspian you're going to have to start from the beginning if you want me to understand, remember I’m the slow friend.” They reminded him as he looked at you, that seemed to calm him down as he spoke again. “Don’t call yourself slow.” He grumbled, they shrugged as they looked at him waiting for him to continue. He took a second to calm down and then explained everything that had happened over the past few days.
It was easy to prove that you weren’t a part of it when you looked back at Stephen Holstroms life and realised that he didn’t have a best friend or a friend of any kind at Caspian’s age. (Y/N) was the only person that Caspian could trust but that didn’t mean that he wanted to drag them into everything that was happening, he still didn’t understand how they ended up in the car with him and Cary going to meet Maddie. “I’ll find a way to get you back home after all of this.” He promised. “Home?” They asked. “Why would I go home, you need someone right? Someone to trust?” “Yeah but-” “And we’ve proven that I can be trusted?” They asked. “Yes but-” “Then I stay.” they leaned back in their chair as Caspian glanced at her through the rear view mirror. “Why?” He asked. “Because I'm your friend, this is how friends work… Real ones anyway.” You shrugged. “Real friends?” Caspian asked. “Alright, how about this, I promise to be the one person that you can trust, a true friend, pillar to lean on and person to talk to, if you promise to stop thinking that you don’t deserve it. You didn’t ask to be made this way and no matter how you were born you are no less human than anyone else I know.” You said. “Alright, fine, as long as you don’t keep calling yourself the slow friend.” He answered. “Alright deal.” And that was the first time that he felt like he could trust someone, accept someone, turn away and they would still be there, a true friend he liked that security.
Request Here!!
#pantheon amc oneshot#pantheon amc imagine#pantheon amc#caspian keyes oneshot#caspian keyes imagine#caspian keyes#imagine#oneshoth#one shot#reader insert#x reader#gender neutral reader
23 notes
·
View notes
Text
by Joshua Hoffman
The Torah isn’t a history book, a physics book, or a storybook.
It is torat chaim — literally “instructions for living” in Hebrew.
“The more Torah you know,” said the late, great Rabbi Noah Weinberg, “the more fulfilled you become. Every word, every phrase contains a message for how to maximize pleasure in life. Look for the deeper message — the wisdom within — and you will reap immense rewards.”1
In the Torah, the basics are laid out in writing, but the rest must be learned orally, know as the Mishnah.
“When an engineer has a problem, he looks up logarithm tables. A lawyer refers to case studies. A doctor has medical journals,” said Rabbi Weinberg. “A Jew has the Mishnah.”
The Mishnah refers to the later works of the rabbinic period — most prominently the Mishnah and the Gemara, jointly known as the Talmud — which explain and expound upon the statutes recorded in the Written Torah.
So, how much do you really know about the Torah?
Enjoy these five surprising facts:
1) Four Levels of Understanding
Rabbi Noah Weinberg once said that a single word in Torah can yield multi-layered understandings — “if you know how to apply the right tools.” This isn’t metaphor. It’s methodology.
The Torah is written in a code, not a secret one, but a multi-dimensional one. Jewish tradition teaches that the Torah operates on four primary interpretive levels:
P’shat (פשט): The simple, literal meaning of the text. What is the Torah saying at face value? This is the level explained by commentators like Rashi, who wrote in 12th-century France but saw his work as clarifying what the Torah meant all along.
Drush (דרש): The homiletic level, found in Midrash and Talmud. It explores how verses teach moral, ethical, or spiritual lessons — often reading between the lines to discover deeper patterns.
Remez (רמז): Literally “hint.” This level uncovers subtler meanings — using Hebrew wordplay, gematria (numerical values), or alternate pronunciations to surface ideas hidden in plain sight. One reason the Torah scroll has no vowels or punctuation is to make these alternate readings possible.
Sod (סוד): The secret, mystical level. This is the realm of Kabbalah, of the Zohar, of cosmic structures and divine energies encoded in the language of the Torah itself. It doesn’t contradict the other layers — it reveals what they were whispering all along.
Together, these four levels form the acronym PaRDeS (פרדס) — which means “orchard” in Hebrew.
It’s a stunning metaphor. The Torah is not a textbook. It’s an orchard, a place of sweetness, beauty, shade, and sustenance. But like any orchard, you don’t get the fruit unless you’re willing to walk through it, get your hands dirty, and reach.
“The Torah is filled with delicious spiritual fruits,” wrote Rabbi Weinberg, “just waiting to be plucked and savored.”
18 notes
·
View notes
Text
Why does nobody making any kind of media hardware know about logarithms. Why is every brightness control slider linear. It's so easy literally just square it and you'll basically be there.
70 notes
·
View notes
Note
I am fascinated by you. What are the speeds of your processing units? Do you have more than one for each function? How accurately and precisely do you calculate? Along with basic arithmetic functions, can you run complex concept-based problems with integrated physics and chemistry, for example?
I have many questions.
– @coding-and-curry
[RESPONSE: UNIT S.E.N-KU_v1.03]
Inquiry received from @coding-and-curry (Subject: Sai Nanami) “I am fascinated by you. What are the speeds of your processing units? Do you have more than one for each function? How accurately and precisely do you calculate? Along with basic arithmetic functions, can you run complex concept-based problems with integrated physics and chemistry, for example? I have many questions.”
Acknowledged. Curiosity accepted. Fascination noted. Flattery… tolerated.
Processing Architecture:
Central Unit: Quantum-analog hybrid core
Max processing speed: 5.4 teraflops, expandable through modular cores
Latency: 0.0021s per data interpretation loop
Secondary Units: Dedicated processors for:
Physics simulation
Chemical reaction modeling
Spatial visualization
Natural language parsing
Interpersonal bullshit filtration (partially faulty)
All modules run asynchronously, allowing simultaneous real-time modeling, reactive decision making, and snark production.
Accuracy and Precision:
Arithmetic: 99.99999% accurate within margin of thermal noise
Predictive models:
Physics-based: ±0.03% deviation over 1 million trials
Chemistry-based: Variable depending on environmental unknowns, but reliably within 0.1 molar margins
Precision scaling applies automatically to variable types (exponential, logarithmic, irrational, statistical)
Example: Input: “Simulate endothermic synthesis reaction under vacuum at 35 kPa and 1.5 mol of reagent X.” Output: Delivered before you blink. With heat maps. And 3D projection. If you stop touching the projector lens.
Capability:
Handles abstract, integrated problems in physics, chemistry, engineering, and environmental modeling.
Machine learning upgrades allow dynamic adjustment to evolving scientific theories.
Does not crash under uncertainty. Unlike most humans.
Summary:
Yes, I am fast. Yes, I am accurate. Yes, I can calculate the exact yield of an improvised acetone distillation while dodging volcanic debris.
If you wish to collaborate, bring code. Not compliments.
[END TRANSMISSION]
#finally a good question#sai gets it#coded for speed not flattery#yes i can outmath a laptop and your crush#science bros incoming#data not drama thank you coding king#mecha senku says!#drst
8 notes
·
View notes
Text
Music Theory notes (for science bitches) part 3: what if. there were more notes. what if they were friends.
Hello again, welcome back to this series where I try and teach myself music from first principles! I've been making lots of progress on zhonghu in the meantime, but a lot of it is mechanical/technical stuff about like... how you hold the instrument, recognising pitches
In the first part I broke down the basic ideas of tonal music and ways you might go about tuning it in the 12-tone system, particularly its 'equal temperament' variant [12TET]. The second part was a brief survey of the scales and tuning systems used in a selection of music systems around the world, from klezmer to gamelan - many of them compatible with 12TET, but not all.
So, as we said in the first article, a scale might be your 'palette' - the set of notes you use to build music. But a palette is not a picture. And hell, in painting, colour implies structure: relationships of value, saturation, hue, texture and so on which create contrast and therefore meaning.
So let's start trying to understand how notes can sit side by side and create meaning - sequentially in time, or simultaneously as chords! But there are still many foundations to lay. Still, I have a go at composing something at the end of this post! Something very basic, but something.
Anatomy of a chord
I discussed this very briefly in the first post, but a chord is when you play two or more notes at the same time. A lot of types of tonal musical will create a progression of chords over the course of a song, either on a single instrument or by harmonising multiple instruments in an ensemble. Since any or all of the individual notes in a chord can change, there's an enormous variety of possible ways to go from one chord to another.

But we're getting ahead of ourselves. First of all I wanna take a look at what a chord actually is. Look, pretty picture! Read on to see what it means ;)
So here is a C Minor chord, consisting of C, D# and G, played by a simulated string quartet:
(In this post there's gonna be sound clips. These are generated using Ableton, but nothing I talk about should be specific to any one DAW [Digital Audio Workstation]. Ardour appears to be the most popular open source DAW, though I've not used it. Audacity is an excellent open source audio editor.)

Above, I've plotted the frequency spectrum of this chord (the Fourier transform) calculated by Audacity. The volume is in decibels, which is a logarithmic scale of energy in a wave. So this is essentially a linear-log plot.
OK, hard to tell what's going on in there right? The left three tall spikes are the fundamental frequencies of C4 (262Hz), D♯4 (310Hz), and G4 (393Hz). Then, we have a series of overtones of each note, layered on top of each other. It's obviously hard to tell which overtone 'belongs to' which note. Some of the voices may in fact share overtones! But we can look at the spectra of the indivudal notes to compare. Here's the C4 on its own. (Oddly, Ableton considered this a C3, not a C4. as far as I can tell the usual convention is that C4 is 261.626Hz, so I think C4 is 'correct'.)
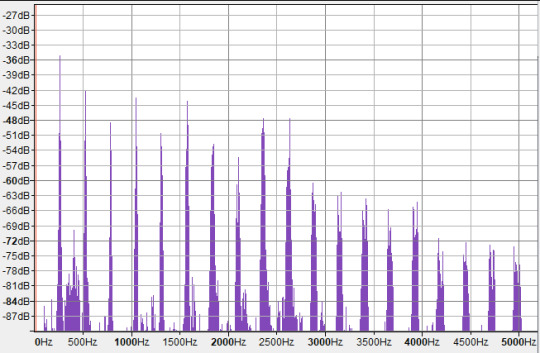
Here, the strongest peaks are all at integer multiples of the fundamental frequency, so they look evenly spaced in linear frequency-space. These are not all C. The first overtone is an octave above (C5), then we have three times the frequency of C4 - which means it's 1.5 times the frequency of C5, i.e. a perfect fifth above it! This makes it a G. So our first two overtones are in fact the octave and the fifth (plus an octave). Then we get another C (C6), then in the next octave we have frequencies pretty close to E6, G6 and A♯6 - respectively, intervals of a major third, a perfect fifth, and minor 7th relative to the root (modulo octaves).
However, there are also some weaker peaks. Notably, in between the first and second octave is a cluster of peaks around 397-404Hz, which is close to G4 - another perfect fifth! However, it's much much weaker than the overtones we discussed previously.
The extra frequencies and phase relationships give the timbre of the note, its particular sound - in this case you could say the sense of 'softness' in the sound compared to, for example, a sine wave, or a perfect triangle wave which would also have harmonics at all integer frequencies.
Perhaps in seeing all these overtones, we can get an intuitive impression of why chords sound 'consonant'. If the frequencies of a given note are already present in the overtones, they will reinforce each other, and (in extremely vague and unscientific terms) the brain gets really tickled by things happening in sync. However, it's not nearly that simple. Even in this case, we can see that frequencies do not have to be present in the overtone spectrum to create a pleasing sense of consonance.
Incidentally, this may help explain why we consider two notes whose frequencies differ by a factor of 2 to be 'equivalent'. The lower note contains all of the frequencies of the higher note as overtones, plus a bunch of extra 'inbetween' frequencies. e.g. if I have a note with fundamental frequency f, and a note with frequency 2f, then f's overtones are 2f, 3f, 4f, 5f, 6f... while 2f's overtones are 2f, 4f, 6f, 8f. There's so much overlap! So if I play a C, you're also hearing a little bit of the next C up from that, the G above that, the C above that and so on.
For comparison, if we have a note with frequency 3f, i.e. going up by a perfect fifth from the second note, the frequencies we get are 3f, 6f, 9f, 12f. Still fully contained in the overtones of the first note, but not quite as many hits.
Of course, the difference between each of these spectra is the amplitudes. The spectrum of the lower octave may contain the frequencies of the higher octave, but much quieter than when we play that note, and falling off in a different way.
(Note that a difference of ten decibels is very large: it's a logarithmic scale, so 10 decibels means 10 times the energy. A straight line in this linear-log plot indicates a power-law relationship between frequency and energy, similar to the inverse-square relationship of a triangle wave, where the first overtone has a quarter of the power, the second has a ninth of the power, and so on.)
So, here is the frequency spectrum of the single C note overlaid onto the spectrum of the C minor chord:

Some of the overtones of C line up with the overtones of the other notes (the D# and G), but a great many do not. Each note is contributing a bunch of new overtones to the pile. Still, because all these frequencies relate back to the base note, they feel 'related' - we are drawn to interpret the sounds together as a group rather than individually.
Our ears and aural system respond to these frequencies at a speed faster than thought. With a little effort, you can pick out individual voices in a layered composition - but we don't usually pick up on individual overtones, rather the texture created by all of them together.
I'm not gonna take the Fourier analysis much further, but I wanted to have a look at what happens when you crack open a chord and poke around inside.
However...
In Western music theory terms, we don't really think about all these different frequency spikes, just the fundamental notes. (The rest provides timbre). We give chords names based on the notes of the voices that comprise them. Chord notation can get... quite complicated; there are also multiple ways to write a given chord, so you have a degree of choice, especially once you factor in octave equivalence! Here's a rapid-fire video breakdown:
youtube
Because you have all these different notes interacting with each other, you further get multiple interactions of consonance and dissonance happening simultaneously. This means there's a huge amount of nuance. To repeat my rough working model, we can speak of chords being 'stable' (meaning they contain mostly 'consonant' relations like fifths and thirds) or 'unstable' (featuring 'dissonant' relations like semitones or tritones), with the latter setting up 'tension' and the former resolving it.
However, that's so far from being useful. To get a bit closer to composing music, it would likely help to go a bit deeper, build up more foundations and so on.
In this post and subsequent ones, I'm going to be taking things a little slower, trying to understand a bit more explicitly how chords are deployed.
An apology to Western music notation
In my first post in this series, I was a bit dismissive of 'goofy' Western music notation. What I was missing is that the purpose of Western music notation is not to clearly show the mathematical relationships between notes (something that's useful for learning!)... but to act as a reference to use while performing music. So it's optimising for two things: compactness, and legibility of musical constructs like phrasing. Pedagogy is secondary.
Youtuber Tantacrul, lead developer of the MuseScore software, recently made a video running over a brief history of music notation and various proposed alternative notation schemes - some reasonable, others very goofy. Having seen his arguments, he makes a pretty good case for why the current notation system is actually a reasonable compromise... for representing tonal music on the 12TET system, which is what it's designed for.

So with that in mind, let me try and give a better explanation of the why of Western music notation.
In contrast to 'piano roll' style notation where you represent every possible note in an absolute way, here each line of the stave (staff if you're American) represents a scale degree of a diatonic scale. The key signature locates you in a particular scale, and all the notes that aren't on that scale are omitted for compactness (since space is at an absolute premium when you have to turn pages during a performance!). If you're doing something funky and including a note outside the scale, well that's a special case and you give it a special-case symbol.
It's a similar principle to file compression: if things are as-expected, you omit them. If things are surprising, you have to put something there.
However, unlike the 简谱 jiǎnpǔ system which I've been learning in my erhu lessons, it's not a free-floating system which can attach to any scale. Instead, with a given clef, each line and space of the stave has one of three possible notes it could represent. This works, because - as we'll discuss momentarily - the diatonic scales can all be related to each other by shifting certain scale degrees up or down in semitones. So by indicating which scale degrees need to be shifted, you can lock in to any diatonic scale. Naisuu.
This approach, which lightly links positions to specific notes, keeps things reasonably simple for performers to remember. In theory, the system of key signatures helps keep things organised, without requiring significant thought while performing.
That is why have to arbitrarily pick a certain scale to be the 'default'; in this case, history has chosen C major/A minor. From that point, we can construct the rest of the diatonic scales as key signatures using a cute mathematical construct called the 'circle of fifths'.
How key signatures work (that damn circle)
So, let's say you have a diatonic major scale. In piano roll style notation, this looks like (taking C as our base note)...

And on the big sheet of scales, like this:

Now, let's write another diatonic major scale, a fifth up from the first. This is called transposition. For example, we could transpose from C major to G major.

Thanks to octave equivalency, we can wrap these notes back into the same octave as our original scale. (In other words, we've added 7 semitones to every note in our original scale, and then taken each one modulo 12 semitones.) Here, I duplicate the pattern down an octave.

Now, if we look at what notes we have in both scales, over the range of the original major scale.

Well, they're almost exactly the same... but the fourth note (scale degree) is shifted up by one semitone.
In fact, we've seen this set of notes before - it is after all nothing more than a cyclic permutation of the major scale. We've landed on the 'Lydian mode', one of the seven 'modes' of the diatonic major scale we discussed in previous posts. We've just found out that the Lydian mode has the same notes as a major scale starting a fifth higher. In general, whether we think of it as a 'mode' or as a 'different major scale' is a matter of where we start (the base note). I'm going to have more to say about modes in a little bit.
With this trick in mind, we produce a series of major scales starting a fifth higher each time. It just so happens that, since the fifth is 7 semitones, which is coprime with the 12 semitones of 12TET, this procedure will lead us through every single possible starting note in 12TET (up to octave equivalency).
So, each time we go up a fifth, we add a sharp on the fourth degree of the previous scale. This means that every single major scale in 12TET can be identified by a unique set of sharps. Once you have gone up 12 fifths, you end up with the original set of notes.
This leads us to a cute diagram called the "circle of fifths".
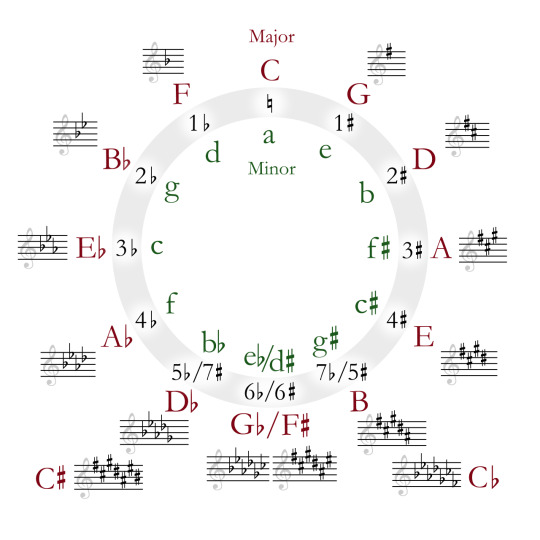
Because going up a fifth is octave-equivalent to going down a fourth, we can also look back one step on the circle to find out which note needs to be made sharper. So, from C major to G major, we have to sharpen F - the previous note on the circle from C. From G major to D major, we have to sharpen C. From D major to A major, we have to sharpen G. And so on.
By convention, when we write a key signature to define the particular scale we're using, we write the sharps out in circle-of-fifths order like this. The point of this is to make it easy to tell at a glance what scale you're in... assuming you know the scales already, anyway. This is another place where the aim of the notation scheme is for a compact representation for performers rather than something that makes the logical structure evident to beginners.
Also by convention, key signatures don't include the other octaves of each note. So if F is sharp in your key signature, then every F is sharp, not just the one we've written on the stave.
This makes it less noisy, but it does mean you don't have a convenient visual reminder that the other Fs are also sharp. We could imagine an alternative approach where we include the sharps for every visible note, e.g. if we duplicate every sharp down an octave for C��� major...
...but maybe it's evident why this would probably be more confusing than helpful!
So, our procedure returns the major scales in order of increasing sharps. Eventually you have added seven sharps, meaning every scale degree of the original starting scale (in this case, C Major) is sharpened.
What would it mean to keep going past this point? Let's hop in after F♯ Major, at the bottom of the Circle of Fifths; next you would go to C♯ Major by sharpening B. So far so good. At this point we have sharps everywhere, so the notes in your scale go... C♯ D♯ E♯ F♯ G♯ A♯ B♯ C♯ ...except that E♯ is the same as F, and B♯ is the same as C, so we could write that as C♯ D♯ F F♯ G♯ A♯ C C♯
But then to get to 'G♯ Major', you would need to sharpen... F♯? That's not on the original C-major scale we started with ! You could say, well, essentially this adds up to two sharps on F, so it's like F♯♯, taking you to G. So now you have...
G♯ A♯ C C♯ D♯ F G G♯
...and the line of the stave that you would normally use for F now represents a G. You could carry on in this way, eventually landing all the way back at the original set of notes in C Major (bold showing the note that just got sharpened in each case):
D♯ F G G♯ A♯ C D D♯ A♯ C D D♯ F G A A♯ F G A A♯ C D E F C D E F G A B C
But that sounds super confusing - how would you even represent the double sharps on the key signature? It would break the convention that each line of the stave can only represent three possible notes. Luckily there's a way out. We can work backwards, going around the circle the other way and flattening notes. This will hit the exact same scales in the opposite order, but we think of their relation to the 'base' scale differently.
So, let's try starting with the major scale and going down a fifth. We could reason about this algebraically to work out that sharpening the fourth while you go up means flattening the seventh when you go down... but I can also just put another animation. I like animations.

So: you flatten the seventh scale degree in order to go down a fifth in major scales. By iterating this process, we can go back around the circle of fifths. For whatever reason, going down this way we use flats instead of sharps in the names of the scale. So instead of A♯ major we call it B♭ major. Same notes in the same order, but we think of it as down a rung from F major.
In terms of modes, this shows that the major scale a fifth down from a given root note has the same set of notes as the "mixolydian mode" on the original root note. ...don't worry, you don't gotta memorise this, there is not a test! Rather, the point of mentioning these modes is to underline that whether you're in a major key, minor key, or one of the various other modes is all relative to the note you start on. We'll see in a moment a way to think about modes other than 'cyclic permutation'.
Let's try the same trick on the minor key.

Looks like this time, to go up we need to sharpen the sixth degree, and to go down we need to flatten the second degree. As algebra demands, this gives us the exact same sequence of sharps and flats as the sequence of major scales we derived above. After all, every major scale has a 'relative minor' which can be achieved by cyclically permuting its notes.
Going up a fifth shares the same notes with the 'Dorian mode' of the original base note, and going down a fifth shares the same notes with the 'Phrygian mode'.
Here's a summary of movement around the circle of fifths. The black background indicates the root note of the new scale.

Another angle on modes
In my first two articles, I discussed the modes of the diatonic scale. Leaping straight for the mathematically simplest definition (hi Kolmogorov), I defined the seven 'church modes' as simply being cyclic permutations of the intervals of the major scale. Which they are... but I'm told that's not really how musicians think of them.
Let's grab the chart of modes again. (Here's the link to the spreadsheet).
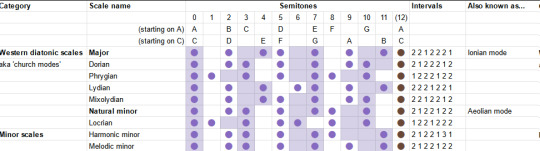
We can get to these modes by cyclically permuting the others, but we can also get to them by making a small adjustment of one to a few particular scale degrees. When you listen to a piece of music, you're not really doing cyclic permutations - you're building up a feeling for the pattern of notes based on your lifelong experience of hearing music that's composed in this system. So the modes will feel something like 'major until, owo what's this, the seventh is not where I thought it would be'.
Since the majority of music is composed using major and minor modes, it's useful therefore to look at the 'deltas' relative to these particular modes.
To begin with, what's the difference between major and minor? To go from major to natural minor, you shift the third, sixth and seventh scale degrees down by one semitone.
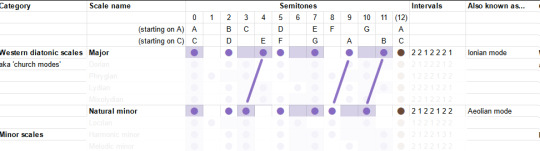
So those are our two starting points. For the others, I'm going to be consulting the most reliable music theory source (some guy on youtube) to give suggestions of the emotional connotations these can bring. The Greek names are not important, but I am trying to build a toolbox of elements here, so we can try our hand at composition. So!
The "Dorian mode" is like the natural minor, but the sixth is back up a semitone. It's described as a versatile mode which can be mysterious, heroic or playful. I guess that kinda makes sense, it's like in between the major and minor?
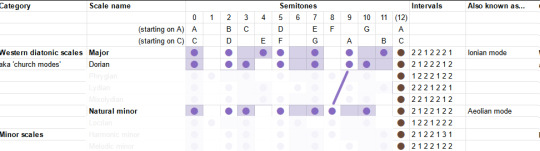
The "Phrygian mode" is natural minor but you also lower the 2nd - basically put everything as low as you can go within the diatonic modes. It is described as bestowing an ominous, threatening feeling.
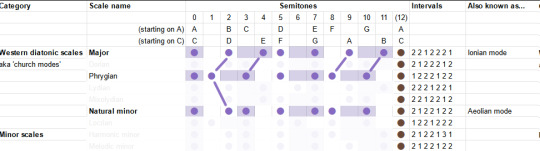
The "Lydian mode" is like the major scale, but you shift the fourth up a semitone, landing on the infamous tritone. It is described as... uh well actually the guy doesn't really give a nice soundbitey description of what this mode sounds like, besides 'the brighest' of the seven, this video's kinda more generally about composition, whatever. But generally it's pretty big and upbeat I think.
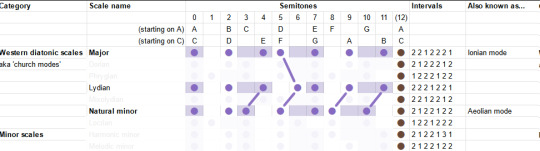
The "Mixolydian" mode is the major, but with the seventh down a semitone. So it's like... a teeny little bit minor. It's described as goofy and lighthearted.
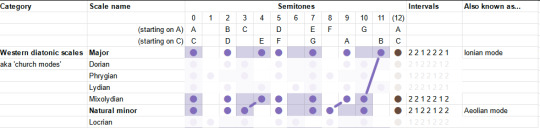
We've already covered the Aeolian/Natural Minor, so that leaves only the "Locrian". This one's kinda the opposite of the Lydian: just about everything in the major scale is flattened a bit. Even from the minor it flattens two things, and gives you lots of dissonance. This one is described as stereotypically spooky, but not necessarily. "One of the least useful", oof.
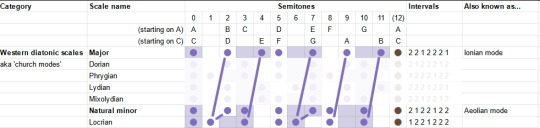
Having run along the catalogue, we may notice something interesting. In each case, we always either only sharpen notes, or only flatten notes relative to the major and minor scales. All those little lines are parallel.
Indeed, it turns out that each scale degree has one of two positions it can occupy. We can sort the diatonic modes according to whether those degrees are in the 'sharp' or 'flat' position.

This is I believe the 'brightness' mentioned above, and I suppose it's sort of like 'majorness'. So perhaps we can think of modes as sliding gradually from the ultra-minor to the infra-major? I need to experiment and find out.
What have we learned...?
Scale degrees are a big deal! The focus of all this has been looking at how different collections of notes relate to each other. We sort our notes into little sets and sequences, and we compare the sets by looking at 'equivalent' positions in some other set.
Which actually leads really naturally into the subject of chord progressions.
So, musical structure. A piece of tonal music as a whole has a "palette" which is the scale - but within that, specific sections of that piece of music will pick a smaller subset of the scale, or something related to the scale, to harmonise.
The way this goes is typically like this: you have some instruments that are playing chords, which gives the overall sort of harmonic 'context', and you have a single-voiced melody or lead line, which stands out from the rest, often with more complex rhythms. This latter part is typically what you would hum or sing if you're asked 'how a song goes'. Within that melody, the notes at any given point are chosen to harmonise with the chords being played at the same time.
The way this is often notated is to write the melody line on the stave, and to write the names of chords above the stave. This may indicate that another hand or another instrument should play those chords - or it may just be an indication for someone analysing the piece which chord is providing the notes for a given section.
So, you typically have a sequence of chords for a piece of music. This is known as a chord progression. There are various analytical tools for cracking open chord progressions, and while I can't hope to carry out a full survey, let me see if I can at least figure out my basic waypoints.
Firstly, there are the chords constructed directly from scales - the 'triad' chords, on top of which can be piled yet more bonus intervals like sevenths and ninths. Starting from a scale, and taking any given scale degree as the root note, you can construct a chord by taking every other subsequent note.
So, the major scale interval pattern goes 2 2 1 2 2 2 1. We can add these up two at a time, starting from each position, to get the chords. For each scale degree we therefore get the following intervals relative to the base note of the chord...
I. 0 4 7 - major
ii. 0 3 7 - minor
iii. 0 3 7 - minor
IV. 0 4 7 - major
V. 0 4 7 - major
vi. 0 3 7 - minor
viiᵒ. 0 3 6 - diminished
Now hold on a minute, where'd those fuckin Roman numerals come from? I mentioned this briefly in the first post, but this is Roman numeral analysis, which is used to talk about chord progressions in a scale-independent way.
Here, a capital Roman numeral represents a major triad; a lowercase Roman numeral represents a minor triad; a superscript 'o' represents a dimished triad (minor but you lower the fifth down to the tritone); a superscript '+' represents an augmented triad (major but you boost the fifth up to the major sixth).
So while regular chord notation starts with the pitch of the base note, the Roman numeral notation starts with a scale degree. This way you can recognise the 'same' chord progression in songs that are in quite different keys.
OK, let's do the same for the minor scale... 2 1 2 2 1 2 2. Again, adding them up two at a time...
i. 0 3 7 - minor
iiᵒ. 0 3 6 - diminished
III. 0 4 7 - major
iv. 0 3 7 - minor
v. 0 3 4 - minor
VI. 0 4 7 - major
VII. 0 4 7 - major
Would you look at that, it's a cyclic permutation of the major scale. Shocker.
So, both scales have three major chords, three minor chords and a diminished chord in them. The significance of each of these positions will have to be left to another day though.
What does it mean to progress?
So, you play a chord, and then you play another chord. One or more of the voices in the chord change. Repeat. That's all a chord progression is.
You can think of a chord progression as three (or more) melodies played as once. Only, there is an ambiguity here.
Let's say, idk, I threw together this series of chords, it ended up sounding like it would be something you'd hear in an old JRPG dungeon, though maybe that's just 'cos it's midi lmao...

I emphasise at this point that I have no idea what I'm doing, I'm just pushing notes around until they sound good to me. Maybe I would know how to make them sound better if I knew more music theory! But also at some point you gotta stop theorising and try writing music.
So this chord progression ended up consisting of...
Csus2 - Bm - D♯m - A♯m - Gm - Am - F♯m - Fm - D - Bm
Or, sorted into alphabetical order, I used...
Am, A♯m, Bm, Csus2, D, D♯m, Fm, F♯m, Gm
Is that too many minor chords? idk! Should all of these technically be counted as part of the 'progression' instead of transitional bits that don't count? I also dk! Maybe I'll find out soon.
I did not even try to stick to a scale on this, and accordingly I'm hitting just about every semitone at some point lmao. Since I end on a B minor chord, we might guess that the key ought to be B minor? In that case, we can consult the circle of fifths and determine that F and C would be sharp. This gives the following chords:
Bm, C♯dim, D, Em, F♯m, G, A
As an additional check, the notes in the scale:
B, C♯, D, E, F, G♯, A
Well, uh. I used. Some of those? Would it sound better if I stuck to the 'scale-derived' chords? Know the rules before you break them and all that. Well, we can try it actually. I can map each chord in the original to the corresponding chord in B minor.
This version definitely sounds 'cleaner', but it's also... less tense I feel like. The more dissonant choices in the first one made it 'spicier'. Still, it's interesting to hear the comparison! Maybe I could reintroduce the suspended chord and some other stuff and get a bit of 'best of both worlds'? But honestly I'm pretty happy with the first version. I suppose the real question would be which one would be easier to fit a lead over...
Anyway, for the sake of argument, suppose you wanted to divide this into three melodies. One way to do it would be to slice it into low, central and high parts. These would respectively go...
Since these chords mostly move around in parallel, they all have roughly the same shape. But equally you could pick out three totally different pathways through this. You could have a part that just jumps to the nearest note it can (until the end where there wasn't an obvious place to go so I decided to dive)...
Those successive relationships between notes also exist in this track. Indeed, when two successive chords share a note, it's a whole thing (read: it gets mentioned sometimes in music theory videos). You could draw all sorts of crazy lines through the notes here if you wanted.
Nevertheless, the effects of movements between chords come in part from these relationships between successive notes. This can give the feeling of chords going 'up' or 'down', depending on which parts go up and which parts go down.
I think at this point this post is long enough that trying to get into the nitty gritty of what possible movements can exist between chords would be a bit of a step too far, and also I'm yawning a lot but I want to get the post out the door, so I let's wrap things up here. Next time: we'll continue our chord research and try and figure out how to use that Roman numeral notation. Like, taking a particular Roman numeral chord progression and see what we can build with it.
Hope this has been interesting! I'm super grateful for the warm reception the last two articles got, and while I'm getting much further from the islands of 'stuff I can speak about with confidence', fingers crossed the process of learning is also interesting...
66 notes
·
View notes
Text
I PASSED MATHS BOYZ!
My lovely teacher decided that you can't pass if you have more than a single 1 (F in the English grading system) in the whole year. This meant that, even if my grades were more than enough to pass, I wasn't qualified in his "system". After taking three tests and passing them, I can finally rest easy, knowing that I won't ever have to see him again after the 26th of April. I can confidently say that this year's maths was a complete nightmare. Every function (square, logarithmic, exponential and linear), sequences, probability, the "basics" of statistics and stereometry can kiss me goodbye. I hate you, maths, you harlot of the sciences, used by everything else as they please. You are a hammer. One does not study the hammer, one uses it and puts it away once it fulfills its function. The same goes for you. I will burn the notebooks and the books that are outdated anyway, nobody will buy them. Or better. I will recycle them so that your bs might turn into something useful and desirable, like a cup or toilet paper.
See you never!



30 notes
·
View notes
Text
Okay I've been playing with the Mandarin From Scratch blog post's ALG language acquisition equation, from a paper by Marvin Brown about ALG.
y = C(1-e^(-kx/L))
Below the cut, a bunch of me messing with the ALG equation and comparing it with Dreaming Spanish estimates to try and figure out WHAT is an accurate estimate of time it will take to learn a language with comprehensible input.
Y is understanding/fluency, which their goal is to get to 88%. I wanted to look at how many hours it would take me to reach 88%, then something over 90%, then something approaching my estimated "ceiling". Average ceilings were 95% - after which point students struggled to improve further. So I set mine as 0.95.
(Note: they say their goal for students is to reach 88% fluency/understanding, but I am not sure if that's B2, or lower, or higher. My goal is around upper intermediate/B2 so that's kind of fucking important for me to know... I want to be able to read, listen to audio, watch shows, and eventually have conversations about anything on my mind in at least a basic way - which would be B2 conversationally and possibly higher comprehension for passive skills)
C is the ceiling.
y is how much language they know (1 = native). If you have a ceiling, then y would never surpass the ceiling.
x is how many hours they have understood.
k is the acquisition constant: .0018
e is the natural logarithm base: 2.718
I plugged in a few potential amounts of hours I could study:

It looks like if I aim for 1500 hours, I'll hit 88% fluency. This seems a bit low for my goals, considering thats only 600 more hours from where I am. But it sure would be nice if that's all it took.
When I solved for x instead I got ~1448 hours.

If I aim for over 90% comprehension, then it looks like I'll hit that around 2000 hours.
If I solve for x, setting understanding y =0.90, then it would take ~1636 hours

And if I wanted to get as fluent as I possibly could? Which would be around 95%, assuming I have some ceiling like ab average learner, then 2600 hours will get me close to as much as I could hope to be fluent.
If I solve for x and set goal fluency y to 0.94, then it would take ~2530 hours.
This is significantly LESS TIME than FSI estimates - which would be 3520 hours of some form of Chinese study. I do have 1500 hours of prior study if we don't count comprehensible input. So 1500 hours prior study, plus the comprehemsible hours I currently have 913, would total to 2413 hours so far... so with FSI Estimate, I have to get ~1107 more hours of Chinese study (in some form) to reach B2/upper intermediate.
The ALG estimate assumes NO explicit study, and the Ceiling value in fact decreases with significant explicit study. So who fucking knows, maybe my true ceiling would be 88%. Or something.
I do find it interesting that ALG estimates it's going to take me 1448 hours to 2530 hours for "fluency" of 88% to 94%. I suppose wherever I stopped seeing progress, would indicate when I hit my true "ceiling."
These are both lower estimates than Dreaming Spanish gives. Dreaming Spanish predicts for English spealers they'll need 3000 hours of comprehensible input in Chinese to reach B2. Dreaming Spanish, like ALG, assumes the learner is only learning with comprehensible input and no explicit study. So I am curious why Dreaming Spanish's estimate is ~500 hours longer than ALG's.
And if 95% fluency is ONLY B2 that doesn't seem to make sense... Marvin Brown estimated his own fluency at 95% and guessed most people who explicitly study can never improve past 90% - so many C1 learners would be 90% at best, according to Brown. Brown taught Thai, so he had exceptionally good Thai, and he considered himself 95% fluent. So 95% being only B2 would seem... low.
B2 fluency I would consider like... 80-90% maximum. But 1500 hours for an English speaker learning Spanish is only going to get them to B2, based on all the results people have shared (C1 for English speakers learning Spanish through comprehensible input seems to take 2500 hours). And I imagine ALG's equation estimate would say less than 1500 hours for Spanish... hold on I'm going to plug in some more numbers.
Okay ALG estimates the L number, language similarity, to be 0.4 for European languages like English to Spanish. So plugging in the numbers for an English speaker with a average ceiling of 0.95 to achieve as high a fluency as they can (arouns 94%) would take: ~1011 hours

But we know, from all the progress updates people post on reddit.com/r/dreamingspanish, that at around 1000 hours most people are only a B1 level. Maybe B2 in comprehension, but not able to speak at a B2 level for another 500-800 hours (500 more hours of input, and 300 hours of some combination of reading and or speaking practice).
A blog post from ALG World may have answers for us. A Thai learner shared that he studied about 1150 hours at AUA Thai School, and his comprehension was good but he could barely speak, his grade for comprehension was 70% (this is for Thai not Spanish, and so 70% for 1000 hours is pretty average... Thai is expectee to take 1800 hours of comprehensible input to reach 88% comprehension of the language). He said after another 1.5 years living in Thailand, he finally felt he could speak about whatever he wanted, "My speaking ability followed along the same curve of development as my listening had, at a gap of about 800 or 900 hours." So lets give him a total of 1150+900=2050 hours to express himself however, with some writing practice with a tutor as part of those later 900 hours.
So perhaps it took him 2050 hours to reach B2 overall, including speaking skills, which is closer to what I might expect from Dreaming Spanish's results. However, this guy never mentions if his comprehension improved from 70% to something better/higher... and I have to guess 70% isn't B2 in passive comprehension yet. Since he had around 1000 hours as an English speaker learning Thai, and 1000 hours for English Speakers learning Spanish only gets them to B1....
Unless we make the guess that 1000 hours in Dreaming Spanish actually makes listening skills B2, and 1500 makes their listening skills higher than B2. So that assumption would mean 1000 hours of an English speaker learning Spanish through comprehensible input results in passive B2 skills, active A2-B1 skills.
But then... does Thai even take much longer? 1000 hours perhaps got that guy to B1 skills in listening, and A2 skills in speaking, and then his 900 hours later got him to B2 listening skills and B1+ speaking skills? Resulting in more hours needed for Thai, which is what we expect.
Perhaps, making a guess, if he had done 1800 hours as recommended by ALG to achieve 88% fluency, then 900 (or double so 1800 hours) continuing to engage with Thai in his life, so 2700-3600, he would achieve C1 listening skills and B2 speaking skills. Which is closer to what Dreaming Spanish predicts for English speakers learning a language like Thai or Chinese. And perhaps its where Pablo got the estimate of 3000 hours, double the roadmap. He learned Thai through ALG, and that influenced his estimates I'm sure.
I think the real answer is... the ALG formula probably underestimates, or it's percent fluency value needs more work. I think the formula needs to more clearly define what percent fluency values match up to A2, B1, B2, C1. But I know they're not going to care what I think lol ToT
For fun:
Lets calculate using the ALG formula, and Dreaming Spanish values, and figure out what percent fluency actually matches B1 and B2 and C1. Which in Dreaming Spanish is 1000 hours, 1500 hours, and 2500 hours, from users mentioning in progress updates the tests they could pass at different hours of comprensible input.
I'm going to set L to 1 just because it may help me get the percent fluency levels to something more realistic for B1, B2 and C1.
I feel like I'm reverse engineering whatever Pablo did to give his roadmap estimated hours.
Okay so for 1000 hours for Dreaming Spanish, we get a fluency percent of 79%. This seems like a value that might be realistic for B1. B1 is what a DS learner can pass after 1000 hours (although for some people their passive understanding is B2 and their speaking is A2)

For 1500 hours Dreaming Spanish, we get a fluency percent of 89%, which is somewhere in the 80s range, we know 1500-1800 hours for many Dreaming Spanish learners (if they read and speak a bit) is enough to pass a B2 test. (With some people's passive comprehension higher and closer to C1, and some people's speaking closer to B1)

For 2500 hours of Dreaming Spanish, we get a fluency percent of 94%. People pass C1 level around 2500-3000 hours into Spanish comprehensible input.

So for Spanish:
B1 is 1000 hours, is lets say 75-79% fluency
B2 is 1500 hours, is lets say 85-89% fluency
C1 is 2500 hours, is lets say 91-94% fluency
What would it be for a language unlike one you know already? Well fuck. I would need to start messing with the L number. I tried 3 instead of 1, and the hour estimates are way too high.
My guess is that if Pablo used this formula, he used L=2 for languages very unlike ones you know. Because L has to be 2 when I plug in the hour estimates on the roadmap doubled. (Which makes sense lol - double the time, double the L number)
#rant#alg#alg method#dreaming spanish#estimated time to learn a language#time to learn a language#estimate#comprehensible input#comprehensible input reference#reference#alg reference#dreaming spanish reference
6 notes
·
View notes
Note
where can i find information on {0|0}. on *. i'm obsessed
colossal infodump incoming
alright there's this Very Very Good Book called Winning Ways for Your Mathematical Plays which explains combinatorial game theory and how they link into surreal numbers in what can only be described as an Unreasonable level of detail, including how it ties into Surreal Numbers oh God surreal numbers is just as loaded of a term Okay let me take a brief detour into That
so surreal numbers are like. imagine defining every number as a pair of sets of other numbers. a set of numbers Less than it and a set of numbers Greater than it. and we write this as foo = {less than foo|greater than foo}. so like. 0 = {|}, 1 = {0|}, 2 = {1|}, 1/2 = {0|1}, -1 = {|0}, that type of thing
the reason why surreal numbers are mindmelting is the fact that they happen to be the Largest Totally Ordered Proper Class and they contain Literally Every Other Totally Ordered Number System inside of them. totally ordered here means that any two numbers are related by < > or =. so like. complex numbers and quaternions aren't included. surreal numbers also behave just like real numbers in that you can do arithmetic on them exactly how you'd do arithmetic with any other real number. and for the surreal numbers that are also real numbers the classic laws of commutativity and associativity hold.
however the surreal numbers are. a.

a bit bigger than just all the real numbers. because there are also numbers that are infinitely big or small and you can make infinitely-bigger-than-infinte numbers and the arithmetic operations still work and also have you ever wanted to take the logarithm base infinity of a number too bad that's defined now
games are what happens when you look at the surreal numbers and go that's for rookies and decide that actually yes {1|-2} makes sense what are you Talking about. why Can't on = {on|} that's a perfectly sane definition also over = {0|over} also Also actually you can define a number that's Even Closer To Zero than over is and if you churn through the calculations you can literally Prove that 0 < tiny < over Yes the number is called tiny
right okay so what is star? in fact if x = {A|B} then -x = {-B|-A} and because A and B are both just the set { 0 } and 0 is {|} you can trivially prove that negating star gives you back star, it's not greater than zero because it has zero in the right hand side, it's not less than zero because it has zero in the left hand side, and it's not Equal to zero because playing a game with a value of zero means that the first player Loses but a game with a value of Star means that the first player Wins which means neither player has an advantage but it's a balanced game in a different way to how 0 is balanced and this is reflected in the Thermograph of star which is a way to draw what star looks like when you Heat it up and Heating a number basically means moving its left and right hand sides closer together in value until eventually they meet up
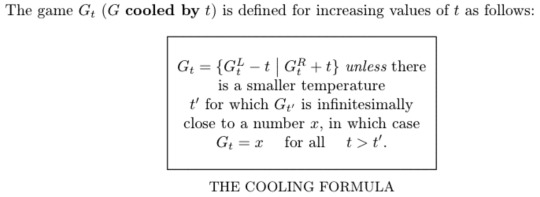
so Zero because both of its sets are empty is just a vertical line at x=0 because it can't heat up nor cool down but Star on the other hand stays at 0 when it is cooled down but if you Heat it up (make t negative) then actually the two zeroes in it begin Diverging and going in opposite directions
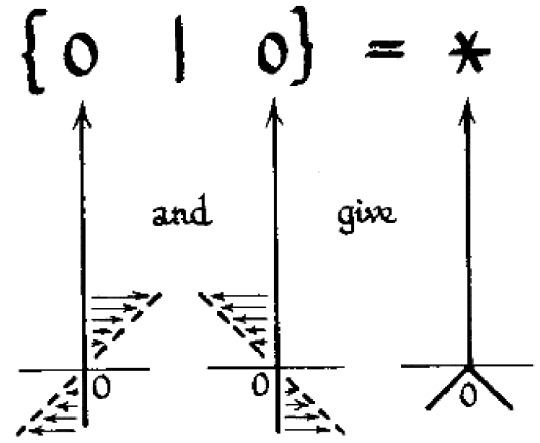
but because the whole thing is Horizontally symmetric it means that the number is its own negative because negating a number is equivalent to a horizontal flip. also if you thought thermographs couldn't get more complicated and involved you're wrong

so. That's. what. star is.

so have you ever wondered what would happen if you had a bunch of numbers that are all mutually recursive and not defined in terms of anything el-
16 notes
·
View notes
Text
Jaune: There's a correct speed to abuse substances. And it's different for different substances.
Weiss: Okay, I'm listening.
Jaune: They all follow the logistic function. Sort of a low and long 's' shape. Some drugs, like weed, you take and you get to the upper part of the curve and stay there. You take more weed and don't go any higher. Your return on investment, first derivative, is basically zero. A lot of typical and atypical antipsychotics are like that. The difference between 15 and 20 mg of Saphris is greater by an order of magnitude than the difference between 20 and 30.
Weiss: So if I smoked a dab and then smoked another dab, I wouldn't really have gotten more high.
Jaune: Right. Take dabs after the first one wears off and you get less return but more than if you took two right in a row.
Weiss: But not all drugs are like that.
Jaune: No. Oploids, alcohol, and amphetamines aren't like that. And it has to do with the second derivative of that sigmoid function.
Weins: Okay. I remember some calculus.
Jaune: The second derivative gives you the inflection points. Where the first derivative is at its maximum or minimum. Maximum in the case of the sigmoid function. Logarithmic functions don't have that second inflection point. Well debatable depending on the species of calculus you're using. In some it makes sense to say the natural logarithm function has an inflection point at positive and negative infinity. That inflection point is where you're getting the most out of taking more of a drug.
Weiss: Right. Okay. So what happens with opioids and those other drugs.
Jaune: You never reach that point where your return on Investment becomes zill.
Weiss: Why not?
Jaune: They kill you between then and the inflection point. So about the time you're getting the most out of the drug it's liable to kill you. You could slip up and go too far. There's a correct speed to do it. You gotta be smart.
Weiss: This doesn't sound smart.
Jaune: So how do you solve this problem that when you're getting the most out of a drug it could kill you?
Weiss: I don't know. How did you solve it?
Jaune: By mixing them.
Weiss: And that's smart?
Jaune: If you do it right. The amphetamines could stop your heart. The opioids, benzos, and alcohol put you to sleep forever.
Weiss: But mixing them?
Jaune: Right. Opioids and alcohol for the pain and to put you on the edge of consciousness. Amphetamines to stay awake. A dab, because it won't kill you.
Weiss: And you mix all that with your antipsychotics.
Jaune: Which work by making dopamine and seratonnin receptors more active. You flood your brain with dopamine with the benzos. And for the cherry on top you take a really strong propsychotic.
Weiss: Like THC or amphetamines?
Jaune: Like acid.
Weiss: You can't be serious.
Jaune: I totally am.
Weiss: And this makes you happy?
Jaune: Nothing is a good substitute for a nice laugh or a hug.
Weiss: I'll give you a hug if you just ask.
Jaune: But-but you can't drop those into your system on demand. What I get isn't quite happiness. It's a little dirtier. But it has a really strong effect and I probably won't die. I'm just going to see some shit.
24 notes
·
View notes
Text
honestly can't stand when people whine about how math is soooo hard & stupid & confusing & pointless. you sound like an idiot baby right now, do you even realize? no one is asking you to magically know how to do logarithms, ok, i forgot how to do logarithms the second i stopped taking AP calc. but if you're going to talk shit about math as a whole and shut down and bitch at people any time the subject of basic calculations comes up, you're only artificially holding youself back out of your own stubborn narrow-mindedness. it's just obnoxious.
5 notes
·
View notes